Reconstructing the Scaffolding A Learner’s Notes on Ordinary Differential Equations

Part Ⅰ Exploring the Picard–Lindelöf and Cauchy–Peano Theorems

The phase portrait of Lotka Volterra equations.

In this blog, I will present detailed mathematical proofs of the Picard–Lindelöf theorem and the Cauchy–Peano existence theorem. This post is part of my ongoing series of learning notes on Ordinary Differential Equations (ODEs), written with the primary goal of strengthening my own understanding and practising the analytical tools I have learned in real analysis and matrix analysis. It would be my pleasure if anyone finds this blog even slightly helpful in their own study of ODEs.

In contrast to more general treatments We warmly recommend the lecture notes provided by Prof. James Burke to readers seeking a more mathematically rigorous treatment of ODE theories., where an ordinary differential equation is expressed as an $ m^{th} $-order $ n \times n $ system $ f(t, \mathbf{x}, \mathbf{x}', \ldots, \mathbf{x}^{(m)}) = 0 $ with $ f $ mapping a subset of $ \mathbb{R} \times (\mathbb{F}^n)^{m+1} $ into $ \mathbb{F}^n $. I will begin with the single-variable case, then move on to vector-valued first-order ODEs, and finally showcase its usage in proving the existence and uniqueness theorem of the general n-th order ODEs and their linear counterparts as supplementary exercises.

Picard-Lindelöf Theorem

Consider the initial value problem (IVP) of the form : $$ \frac{dy}{dt} = f(t,y), y(t_0) = y_0 $$ where $ f(t, y) $ is a function defined in some region of the $ (t, y) $-plane containing the initial point $ (t_0, y_0) $. If $ f(t, y) $ is continuous in $ t $ and Lipschitz continuous in $ y $ in a rectangular region $ R = \{ (t, y) : |t - t_0| \le a, |y - y_0| \le b \} $, where $ a $ and $ b $ are positive constants. Then, there exists a unique solution $ y(t) $ to the IVP, defined on some interval $ [t_0 - h, t_0 + h] $ for some $ h > 0 $.

Lipschitz Continuity A function $ f(t, y) $ is Lipschitz continuous in $ y $ if there exists a constant $ L_f > 0 $ (called the Lipschitz constant) such that: $$ |f(t, y_1) - f(t, y_2)| \leq L_f |y_1 - y_2| $$ for all $ (t, y_1), (t, y_2) \in R $. It’s stronger than continuity but weaker than differentiability—most differentiable functions with bounded derivatives are Lipschitz continuous.

Proof:

Step 1: The IVP $ \frac{dy}{dt} = f(t, y) $, $ y(t_0) = y_0 $ is equivalent to the integral equation by the Fundamental Theorem of Calculus $ y(t) = y_0 + \int_{t_0}^t f(s, y(s)) \, ds $.

Step 2: Picard's Iteration: Define a sequence of functions $ \{ y_n(t) \} $ to approximate the solution: Start with $ y_0(t) = y_0 $ (the constant initial condition). For $ n \geq 0 $, define: $$ y_{n+1}(t) = y_0 + \int_{t_0}^t f(s, y_n(s)) \, ds $$

Step 3: Pick $ h \leq \min\left\{a, \frac{b}{M} \right\} $ such that the sequence of functions $ \{ y_n(t) \} $ is well-defined on the interval $ [t_0 - h, t_0 + h] $, where $$ M = \sup_{(t, y) \in R} |f(t, y)| < \infty $$ since $ f $ is continuous and $ R $ is bounded (compact). Specifically, $ |y(t) - y_0| \leq \int_{t_0}^t |f(s, y(s))| \, ds \leq Mh < b $.

Step 4: Use Banach Fixed-Point Theorem to prove convergence. Define the operator $ T $ on the space of continuous functions $ \mathcal{C}[t_0 - h, t_0 + h] $ with the supremum norm $ \|y\|_{\infty} = \sup_{t} |y(t)| $, guaranteeing a complete metric space (i.e., every Cauchy sequence is convergent): $$ T \left[ y \right]\left(t \right) = y_0 + \int_{t_0}^t f(s, y(s)) \, ds. $$ We’ll show $ T $ is a contraction mapping, meaning there exists $ 0 < \lambda < 1 $ such that: $ \| T[y] - T[z] \|_{\infty} \le \lambda \| y - z \|_{\infty} $. The Banach fixed-point theorem then guarantees the sequence $ y_{n+1} = T[y_n] $ converges to a unique fixed point $ y = T[y] $, satisfying the integral equation and hence the IVP. For any $ y, z \in C[t_0 - h, t_0 + h] $: $$ |T[y](t) - T[z](t)| = \left| \int_{t_0}^t [f(s, y(s)) - f(s, z(s))] \, ds \right| \leq \int_{t_0}^t |f(s, y(s)) - f(s, z(s))| \, ds $$ Using the Lipschitz condition: $$ |f(s, y(s)) - f(s, z(s))| \leq L_f |y(s) - z(s)| \leq L_f \| y - z \|_{\infty} $$ Thus, $$ \begin{align*} |T[y]\left(t \right) - T[z]\left(t \right)| &\le \int_{t_0}^t L_f \| y - z \|_{\infty} \, ds = L_f \| y - z \|_{\infty} |t - t_0| \\ &\le L_f h \| y - z \|_{\infty} \; \text{since} \: |t - t_0| \le h. \end{align*} $$ Taking the supremum: $ \| T[y] - T[z] \|_{\infty} \leq L_f h \| y - z \|_{\infty} $. If $ L_f h < 1 $ (e.g., choosing $ h < \min\{ a, \frac{b}{M}, \frac{1}{L_f} \} $), then $ \lambda = L_f h < 1 $, and $ T $ is a contraction mapping.

The single variable case of Picard-Lindelöf Theorem can be easily generalised to vector-valued ODEs: $$ \frac{d\mathbf{x}}{dt} = f(t, \mathbf{x}), \quad \mathbf{x}(0) = \mathbf{x}_0, $$ where $ t \in [0, T] $ for some fixed $ T > 0 $, $ \mathbf{x}(t) \in \mathbb{R}^d $, $ f = (f_1, \ldots, f_d) : D \subset [0, T] \times \mathbb{R}^d \to \mathbb{R}^d $ is continuous and Lipschitz continuous with respect to $ \mathbf{x} $, i.e., $$ \| f(t, \mathbf{x}) - f(t, \mathbf{y}) \| \leq L_f \| \mathbf{x} - \mathbf{y} \|, \quad \forall (t, \mathbf{x}), (t, \mathbf{y}) \in D, $$ $ \mathbf{x}_0 \in \mathbb{R}^d $ is the initial condition at $ t = 0 $.Technically, this is a forward time version. A backward-in-time version (on $ [t_0 - a, t_0] $) can be proved in a similar fashion by simply using $ \widetilde{x}(t) = x(c - t) $, and correspondingly $ \widetilde{f}(t) = -f(c-t, x) $. A solution can be viewed as a parametric curve in an n-dimensional space while $ t $ changing in the interval $ [0, T] $. It can also be viewed as a trajectory of a particle moving in an n-dimensional space with its velocity (i.e., the tangent vector of the path) specified as per $ f(t, \mathbf{x}) $.

The mathematical proof is almost identical to that of the single variable case, provided the vector norm $ \| \cdot \| $ is used instead to replace the absolute value $ | \cdot | $.

Step 1: Construct a compact set $ R = [0, h] \cap [0, T] \times \overline{B}(\mathbf{x}_0, r) $ (hypercylinder) and a contraction operator $$ \Phi[\mathbf{x}]\left(t \right) = \mathbf{x}_0 + \int_{t_0}^t f(s, \mathbf{x}(s))ds, $$ where $ h \leq \frac{r}{M} $ and $ M = \sup_{ (t, \mathbf{x}) \in R} \| f(t, \mathbf{x}) \| < \infty $, ensuring $ \| \Phi[\mathbf{x}]\left(t \right) - \mathbf{x}_0 \| \leq r $ for all $ t \in [0, h] $.

Step 2: $$ \| \Phi[\mathbf{x}](t) - \Phi[\mathbf{y}](t)\| = \| \int_0^t \left[ f(s, \mathbf{x}(s)) - f(s, \mathbf{y}(s))ds \right] \| \leq \int_0^t L_f \| \mathbf{x}(s) - \mathbf{y}(s) \| ds $$ Define the supremum norm on $ \mathcal{C}([0, T];\mathbb{R}^d) $ as $ \| \mathbf{x} \|_{\infty} = \sup_t \| \mathbf{x}(t) \| $, and then take $ \sup $ gives $$ \| \Phi[\mathbf{x}] - \Phi[\mathbf{y}] \|_{\infty} \le L_f h \| \mathbf{x} - \mathbf{y} \|_{\infty}. $$ Thus if we choose $ h < \frac{1}{L_f} $, then $ \Phi[\cdot] $ is a contraction mapping.

Step 3: By Banach Fixed-Point Theorem, $ \Phi $ has a unique fixed point $ \mathbf{x} $ such that: $$ \mathbf{x}(t) = \mathbf{x}_0 + \int_0^t f(s, \mathbf{x}(s))ds, \quad t \in [0, h], \; \text{where} \; h = \min \{ \frac{r}{M}, \frac{1}{L_f} \} $$

In the following, we give another proof where the property of uniform convergence is used.

In the Picard's Iteration $ \mathbf{x}_0(t) \equiv \mathbf{x}_0, \mathbf{x}_{n+1}(t) = \mathbf{x}_0 + \int_0^t f(s, \mathbf{x}_n(s)) ds $ $$ \begin{align*} \| \mathbf{x}_1(t) - \mathbf{x}_0(t) \| &= \| \int_0^t f(s, \mathbf{x}_0(s)) ds \| \leq Mt \\ \| \mathbf{x}_2(t) - \mathbf{x}_1(t) \| &= \| \int_0^t \left[ f(s, \mathbf{x}_1(s)) - f(s, \mathbf{x}_0(s)) ds \right] \| \leq \int_0^t L_f \| \mathbf{x}_1(s) - \mathbf{x}_0(s) \| ds \\ &\leq M L_f \int_0^t s ds = M L_f \frac{t^2}{2}\\ \| \mathbf{x}_3(t) - \mathbf{x}_2(t) \| &= \| \int_0^t \left[ f(s, \mathbf{x}_2(s)) - f(s, \mathbf{x}_1(s)) ds \right] \| \leq \int_0^t L_f \| \mathbf{x}_2(s) - \mathbf{x}_1(s) \| ds \\ &\leq ML_f^2 \int_0^t \frac{s^2}{2} ds = ML_f^2 \frac{t^3}{3!}\\ & \vdots \\ \| \mathbf{x}_{n}(t) - \mathbf{x}_{n-1}(t) \| & \leq M L_f^{n-1} \frac{t^{n}}{n!} \leq M L_f^{n-1} \frac{h^{n}}{n!} \end{align*} $$ $$ \sum_{i=1}^{n} \| \mathbf{x}_{i}(t) - \mathbf{x}_{i-1}(t) \| \leq \frac{M}{L_f} \underbrace{\sum_{i=1}^n \frac{(KL_f)^i}{i !}}_{e^{L_f h} - 1} $$

By Weierstrass M-Test, series $ \sum_{i=1}^{n} \| \mathbf{x}_{i}(t) - \mathbf{x}_{i-1}(t) \| $ converges uniformly on $ [0, h] $, implying $ \| \mathbf{x}_{n}(t) \| \le \| \mathbf{x}_0(t) \| + \sum_{i=1}^{n} \| \mathbf{x}_{i}(t) - \mathbf{x}_{i-1}(t) \| $ converges uniformly to $ \mathbf{x}(t) $ on $ [0, h] $. As $ R $ is compact, $ f $ is continuous and thus uniform continuous, implying that $ f(t, \mathbf{x}_{n}(t)) $ converges uniformly to $ f(t, \mathbf{x}(t)) $. Furthermore, the uniform convergence guarantees $ \lim_{n} \int_a^b f_n(t) dt = \int_a^b f(t) dt $, where $ f_n \to f $ uniformly on $ R = [0, h] \cap [0, T] \times \overline{B}(\mathbf{x}_0, r) $ and $ f_n $ is integrable.

Therefore, we can conclude that $$ \lim_n \mathbf{x}_{n+1}(t) = \mathbf{x}_0 + \lim_n \int_0^t f(s, \mathbf{x}_n(s)) ds = \mathbf{x}_0 + \int_0^t \lim_n f(s, \mathbf{x}_n(s)) ds $$ $$ \mathbf{x}(t) = \mathbf{x}_0 + \int_0^t f(s, \mathbf{x}(s)) ds $$

The uniqueness of the solution can be proved by Grönwall's Lemma. Let $ u \in \mathcal{C}([0, T]) $. If there exist two constants $ \alpha, \beta \in \mathbb{R}, \beta \geq 0 $, such that $ u(t) \leq \alpha + \beta \int_0^t u(s) ds, \; t \in [0, T] $, then $ u(t) \leq \alpha e^{\beta t} $ for all $ t \in [0, T] $.

Proof:

Let $ v(t) := \alpha + \beta \int_0^t u(s) ds $. Then $ u \le v $ and $ v^{\prime}(t) = \beta u(t) \leq \beta v(t) $. Solve $ v^{\prime}(t) \le \beta v(t) $ to get $ u(t) \le v(t) \leq \alpha e^{\beta t} $. If there exist two solutions $ \mathbf{x}_1(t), \mathbf{x}_2(t) $ that both satisfy $ \mathbf{x}^{\prime}(t) = f(t, \mathbf{x}(t)), \mathbf{x}(0) = \mathbf{x}_0 $, then $$ \| \mathbf{x}_1(t) - \mathbf{x}_2(t) \| = \| \int_0^t \left[ f(s, \mathbf{x}_1(s)) - f(s, \mathbf{x}_2(s)) \right] ds \| \leq L_f \int_0^t \| \mathbf{x}_1(s) - \mathbf{x}_2(s) \| ds $$ Set $ u(t) = \| \mathbf{x}_1(t) - \mathbf{x}_2(t) \| $, then by Grönwall's Lemma, $ \| \mathbf{x}_1(t) - \mathbf{x}_2(t) \| = 0 $.

Maximal Interval of Existence and Continuation Given $ (t_0, \mathbf{x}_0) $, there exists a unique maximal solution: $ (t_0, \tau_{+}) \to \mathbb{R}^d $ with $ t_0 < \tau_{+} \le T $, obtained by extending the local solution as long as it remains in $ [t_0, T] \times \mathbb{R}^d $ and within regions where $ f $ is continuous and locally Lipschitz in $ \mathbf{x} $. If $ \tau_{+} \le T $, then necessarily $ \lim_{t \to \tau_{+}} \| x(t) \| \to \infty $ or $ x(t) $ approaches a point where $ f $ ceases to be continuous or locally Lipschitz in $ \mathbf{x} $. In particular, if the solution remains bounded (not blow-up in finite time) and $ f $ is continuous and locally Lipschitz in $ \mathbf{x} $ on all of $ [t_0, T] \times \mathbb{R}^d $, the solution can be extended to the right point $ T $.

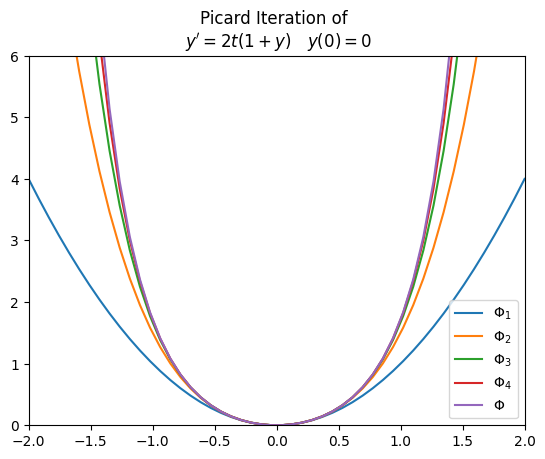
Next, let us take a quick look at a simple example The example is borrowed from the book Elementary Differential Equations and Boundary Value Problems. to gain an intuitive understanding of how Picard's iteration works: $$ y' = 2t(1 + y), \quad y(0) = 0 $$

Applying the Picard's iteration $ \Phi_{n+1}(t) = y_0 + \int_0^t f(s, \Phi_n(s)) ds $ to $ f(t, y(t)) = 2t(1 + y) $, we obtain: $$ \Phi_n(t) = \sum_{k=1}^n \frac{t^{2k}}{k!} $$

Proof by induction. For $ n = 1 $, $ \Phi_1(t) = \int_0^t 2s\left(1 + \Phi_0(s) \right) ds = t^2 $, where $ \Phi_0(t) = 0 $. We then need to show that if it is true for $ n = k $, then it also holds true for $ n = k + 1 $. $$ \begin{align*} \Phi_{k+1}(t) &= \int_0^t 2s \left( 1 + \Phi_k(s) \right) ds \\ &= \int_0^t 2s \left( 1 + s^2 + \frac{s^4}{2!} + \cdots + \frac{s^{2k}}{k!} \right) ds\\ &= \int_0^t 2s + 2s^3 + \frac{2s^5}{2!} + \cdots + \frac{2s^{2k+1}}{k!} ds \\ &= t^2 + \frac{t^4}{2!} + \frac{t^6}{3!} + \cdots + \frac{t^{2k+2}}{(k+1)!} \end{align*} $$ The infinite series $ \sum_{k=1}^{\infty} \frac{t^{2k}}{k!} $ converges to $ \Phi(t) = e^{t^2} - 1 $.

Cauchy-Peano Existence Theorem

For the initial value problem $$ \begin{cases} \mathbf{x}^{\prime}(t) = f(t, \mathbf{x}(t)), \quad t \in [0, T], \\ \mathbf{x}(t_0) = \mathbf{x}_0 \in \mathbb{R}^d \end{cases} $$ where $ f : [0, T] \times \mathbb{R}^d \to \mathbb{R}^d $ is continuous. Then there exists a solution $ \mathbf{x}(t) \in \mathcal{C}^1([t_0, t_0 + h]; \mathbb{R}^d) $ that satisfies both the differential equation and the initial condition.

Proof:

Step 1: Define a compact set $ R = [t_0, t_0 + h] \cap [0, T] \times \overline{B}(\mathbf{x}_0, r) $, where $ h \le \frac{r}{M} $ and $ M = \sup_{ (t, \mathbf{x}) \in \mathbb{R}^d} \| f(t, \mathbf{x}) \| < \infty $, to ensure $ \| \mathbf{x}(t) - \mathbf{x}_0 \| \le \| \int_0^t f(s, \mathbf{x}(s)) ds \| \le r $.

Step 2: Construct a sequence of piecewise linear functions $ \mathbf{x}_n(t) $, called Euler polygons, to approximate the solution over $ [t_0, t_0 + h] $. Specifically, for each positive integer $ n $:

Divide $ [t_0, t_0 + h] $ into $ n $ equal subintervals of length $ \Delta_n = \frac{h}{n} $, with points $ t_k^n = t_0 + k \Delta_n $ for $ k = 0, 1, \ldots, n $.
Set $ \mathbf{x}_n(t_0) = \mathbf{x}_0 $.
On each subinterval $ [t_k^n, t_{k+1}^n] $, define $ \mathbf{x}_n(t) $ linearly with slope $ f(t_k^n, \mathbf{x}_n(t_k^n)) $: $ \mathbf{x}_n(t) = \mathbf{x}_n(t_k^n) + f(t_k^n, \mathbf{x}_n(t_k^n))(t - t_k^n) \quad \text{for} \quad t \in [t_k^n, t_{k+1}^n] $.

Step 3: To prove local existence of a solution, we then apply Arzelà–Ascoli theorem, which states that that a sequence of functions $ \{ f_n \}_1^{\infty} \in \mathcal{C}(X) $, where $ X $ denotes a compact metric space with the supremum norm $ \| f \|_{\infty} = \sup_{x \in X} | f(x) | $ has a uniformly convergent subsequence if it is bounded and equicontinuous. Specifically, $ \{ f_n \}_1^{\infty} \in \mathcal{C}(X) $ is bounded means that there exists a positive constant $ M < \infty $ such that $ | f_n(x) | < M $ for each $ x \in X $ and each $ f_n $. $ \{ f_n \}_1^{\infty} \in \mathcal{C}(X) $ is equicontinuous at a point $ a \in X $ means that, for each $ \epsilon > 0 $, there exists $ \delta > 0 $ such that $ |f_n(x) - f_n(a) | < \epsilon $ for all $ x \in X $ with $ \text{dist}(x, a) < \delta $ and for all $ f_n $, which means $ \delta $ is independent of functions. Furthermore, If $ X $ is compact and a family of functions $ \mathcal{F} \in \mathcal{C}(X) $ is equicontinuous on $ X $, then $ \mathcal{F} $ is uniformly equicontinuous, which means that, for each $ \epsilon > 0 $, there exists $ \delta > 0 $ such that $ | f(x) - f(y) | < \epsilon $ for all $ x, y \in X $ with $ \text{dist}(x, y) < \delta $ and for all $ f \in \mathcal{F} $.

In our case $ \mathbf{x}_n(t) \in \mathcal{C}([0, T]; \mathbb{R}^d) $, we need to prove the (uniform) boundedness and equicontinuity of $ \mathbf{x}_n $. Then there exists a subsequence $ \{ \mathbf{x}_{n_k} \} $ converging uniformly to some $ \mathbf{x} \in \mathcal{C}([0, T]; \mathbb{R}^d) $.

Uniform boundedness. For each $ n $ and $ t \in [t^n_k, t^n_{k+1}] $, $$ \| \mathbf{x}_n(t) - \mathbf{x}_0 \| \le \sum_{j=0}^{k-1} \| \mathbf{x}_n(t_{j+1}^n) - \mathbf{x}_n(t_{j}^n) \| + \| \mathbf{x}_n(t) - \mathbf{x}_n(t_k^n) \| \leq \sum_{j=0}^{k-1} M \Delta_n + M | t - t_k^n | \leq M | t - t_0 | \leq Mh $$
Equicontinuity. For $ s, t \in [t^n_k, t^n_{k+1}] $ with $ s < t $, $$ \| \mathbf{x}_n(t) - \mathbf{x}_n(s) \| \leq \int_s^t \| f(t_k^n, \mathbf{x}_n(t_k^n)) \| du \leq M | t - s | $$

Unlike Picard–Lindelöf, the Cauchy-Piano Existence theorem does not assume Lipschitz continuity in $ \mathbf{x} $, so the uniqueness is not guaranteed. A classical example in $ d = 1 $ is $ x'(t) = \sqrt{|x(t)|}, \; x(0) = 0 $. Here $ f(x) = \sqrt{|x|} $ is continuous but not Lipschitz at $ 0 $ (the derivative of $ \sqrt{|x|} $ is unbounded near zero). For any $ \tau \ge 0 $, $$ x_{\tau}(t) = \begin{cases} 0, \; 0 \le t \le \tau, \\ \frac{(t - \tau)^2}{4}, \; t \ge \tau, \end{cases} $$ is a $ C^1 $ solution. Thus there are infinitely many solutions passing through $ (0, 0) $.

The General N-th Order ODE

Next, we consider the IVP of the general n-th order ODE: $$ \begin{cases} y^{(n)}(t) = F(t, y(t), y'(t), \ldots, y^{(n-1)}(t)), \quad t \in [0, T], \\ y(t_0) = y_0, y'(t_0) = y_1, \ldots, y^{(n-1)}(t_0) = y_{n-1}, \end{cases} $$ where $ F : [0, T] \times \mathbb{R}^n \to \mathbb{R} $ is continuous in $ t $ and Lipschitz continuous w.r.t. the other variables, i.e., $ | F(t, \mathbf{x}) - F(t, \mathbf{z}) | \leq L \| \mathbf{x} - \mathbf{z} \| $. Then, there exists a unique function $ y \in \mathcal{C}^n(J), \; J := [t_0 - h, t_0 + h] \cap [0, T] $ solving the IVP.

We will show that the n-th order ODE can be transformed to a system of n first-order ODEs, then apply the Picard-Lindelöf theorem derived above regarding systems of first-order ODEs to conclude the proof.

Define $ x_1(t) := y(t), x_2(t) := y'(t), x_3(t) := y''(t), \ldots, x_n(t) := y^{(n-1)}(t) $. Then $$ \begin{align*} x'_1 &= x_2 \\ x'_2 &= x_3 \\ &\vdots \\ x'_{n-1} &= x_n \\ x'_n &= F(t, x_1, x_2, \ldots, x_n) \end{align*} $$ Write this compactly as the first-order system: $$ \begin{cases} \mathbf{x}'(t) = f(t, \mathbf{x}(t)) \\ \mathbf{x}(t_0) = \mathbf{x}_0 : = (y_0, y_1, \ldots, y_{n-1})^T \end{cases} $$ where $ f : [0, T] \times \mathbb{R}^n \to \mathbb{R}^n $ is defined by $ f(t, \mathbf{x}) := (x_2, x_3, \ldots, x_n, F(t, \mathbf{x}))^T, \; \mathbf{x} = (x_1, \ldots, x_n)^T \in \mathbb{R}^n $.

It is trivial to check that $ f $ is continuous as its components are continuous. We just need to verify the Lipschitz continuity in $ \mathbf{x} $. For $$ (t, \mathbf{x}), (t, \mathbf{z}) \in \widetilde{\mathcal{R}} := ([t_0 - h, t_0 + h] \cap [0, T]) \times \overline{B}(\mathbf{x}_0, r) \subset [0, T] \times \mathbb{R}^n, $$ $$ \begin{align*} \| f(t, \mathbf{x}) - f(t, \mathbf{z}) \| &= \| (x_2 - z_2, \ldots, x_n - z_n, F(t, \mathbf{x}) - F(t, \mathbf{z})) \| \\ &\le \| \mathbf{x} - \mathbf{z} \| + | F(t, \mathbf{x}) - F(t, \mathbf{z}) | \leq (1 + L) \| \mathbf{x} - \mathbf{z} \| \end{align*} $$

By the Picard–Lindelöf theorem proved previously for a system of first-order ODEs, there exists a unique solution $ \mathbf{x}(t) \in \mathcal{C}^1(J;\mathbb{R}^n) $ of the system $ \mathbf{x}'(t) = f(t, \mathbf{x}(t)) $ with the initial condition $ \mathbf{x}(t_0) = \mathbf{x}_0 : = (y_0, y_1, \ldots, y_{n-1})^T $ on $ J := [t_0 - h, t_0 + h] \cap [0, T] $, where $ h \le \{ \frac{r}{\widetilde{M}}, \frac{1}{L} \} $ and $ \widetilde{M} = \sup | f(t, \mathbf{x}) | < \infty $. As $ \mathbf{x} \in \mathcal{C}^1(J) $, $ x_n = y^{(n-1)} \in \mathcal{C}^1(J) $, implying $ y^{(n)} \in \mathcal{C}^n(J) $.

N-th Order Linear ODEs

For n-th order linear ODEs $ y^{(n)} + p_1(t)y^{(n-1)} + \cdots + p_{n-1}(t)y' + p_n(t)y = g(t) $ with initial conditions $ y(t_0) = y_0, y'(t_0) = y_1, \ldots, y^{(n-1)}(t_0) = y_{n-1} $, where $ t_0 \in I := (a, b) $ and $ p_1(t), \ldots, p_n(t), g(t) $ are continuous on the open interval $ I $, then there exists a unique solution $ y = \phi(t) $ that satisfies the IVP and exists throughout the interval $ I $.

Similarly, we can convert n-th order linear ODEs to a system of first-order ODEs $ \mathbf{x}' = \mathbf{A}(t)\mathbf{x} + \mathbf{g}(t) $, where $$ \mathbf{A}(t) = \begin{pmatrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ -p_n(t) & -p_{n-1}(t) & -p_{n-2}(t) & \cdots & -p_1(t) \end{pmatrix}. $$ and $ \mathbf{g}(t) = (0, 0, \ldots, 0, g(t))^T $, with initial conditions $ \mathbf{x}(t_0) = \mathbf{x}_0 := (y_0, y_1, \ldots, y_{n-1})^T $.

To apply the Picard–Lindelöf theorem, we need to check two conditions of $ f(t, \mathbf{x}) = \mathbf{A}(t)\mathbf{x} + \mathbf{g}(t) $:

Continuity. The entries of $ \mathbf{A}(t) $ are continuous functions $ p_i(t) $ and thus $ \mathbf{A}(t) $ is continuous ($ \| \mathbf{A}(t_1) - \mathbf{A}(t_2) \| \le \sum_{i,j} \left[a_{ij}(t_1) - a_{ij}(t_2) \right]^2 $, where the matrix norm is defined by $ \| \mathbf{A} \| = \max_{\| \mathbf{x} \|=1} \| \mathbf{Ax} \|, \;\text{where}\; \mathbf{x} \in \mathbb{R}^n $). $ \mathbf{g}(t) $ is continuous as the only contained entry $ g(t) $ is continuous as specified.
Lipschitz continuity. $$ \| \mathbf{f}(t, \mathbf{x}) - \mathbf{f}(t, \mathbf{y}) \| = \| \mathbf{A}(t) \mathbf{x} + \mathbf{g}(t) - (\mathbf{A}(t) \mathbf{y} + \mathbf{g}(t)) \| = \| \mathbf{A}(t) (\mathbf{x} - \mathbf{y}) \| \le \| \mathbf{A}(t) \| \| \mathbf{x} - \mathbf{y} \|. $$ The matrix norm is bounded (e.g., $ \| \mathbf{A} \|_{\infty} = \max_i \sum_j | a_{ij} | $, and matrix norms are equivalent.), say by $ K $, since each entry $ p_i(t) $ is a continuous function on a compact interval ($ | p_i(t) | < M_i $). Thus, $ \| f(t, \mathbf{x}) - f(t, \mathbf{y}) \| \leq K \| \mathbf{x} - \mathbf{y} \| $.

The Picard-Lindelöf theorem guarantees a local solution $ \mathbf{x}(t) $ existing on some interval $ [t_0 - h, t_0 + h] \subset I $. Since the ODE is linear, we can extend the solution to the entire interval $ I $. $$ \| \mathbf{x}(t) \| \leq \| \mathbf{x}_0 \| + \int_{t_0}^t [ \| \mathbf{A}(s) \| \| \mathbf{x}(s) \| + \| \mathbf{g}(s) \| ] \, ds. $$ Since $ \| \mathbf{A}(s) \| \le K $ and $ \| \mathbf{g}(s) \| \le M_g $ on $ I $, apply Grönwall’s inequality. $$ \| \mathbf{x}(t) \| \leq \left( \| \mathbf{x}_0 \| + M_g| t - t_0 | \right)e^{K| t - t_0 |} $$

Therefore, the solution remains bounded in the interval. Suppose the maximal interval of existence has a right endpoint $ \beta < b $. Since $ p_i(t), g(t) $ are continuous on $ I $, they are continuous on any compact subinterval $ [t_0, \beta + \epsilon] \subset I $. Reapply Picard-Lindelöf at $ t = \beta $, using $ \mathbf{x}(\beta) $ as the new initial condition. This extends the solution beyond $ \beta $, contradicting the maximality of $ \beta $. Thus, the solution extends to $ b $. Similarly, it extends to the left endpoint $ a $. Furthermore, any two solutions defined on overlapping intervals must coincide as their difference satisfies the homogeneous equation $ \mathbf{A}(t)\mathbf{x} = \mathbf{0} $, which has a unique solution $ \mathbf{x}(t) = \mathbf{0} $. Thus, the solution is unique across $ I $.

Actually, $ f(t, \mathbf{x}) = \mathbf{A}(t)\mathbf{x} + \mathbf{g}(t) $ is a special case of a common sufficient condition for global existence on the full interval $ [0, T] $, i.e., a linear growth bound: $$ \| f(t, \mathbf{x}) \| \le a(t) + b \| \mathbf{x} \|, \; t \in [0, T], \mathbf{x} \in \mathbb{R}^d, $$ with $ a \in L^1([0, T]) $ and $ b\ge 0 $. By Grönwall's inequality, $ \| \mathbf{x}(t) \| \le \left(\|\mathbf{x}_{0}\| + \int_{t_0}^t a(s)ds \right)e^{b(t - t_0)}, \; t \ge t_0 $. This bound prevents blow-up in finite time, so the solution can be extended to the end point $ T $.

Concluding Remarks

It is not uncommon for mathematics textbooks to omit certain steps in their proofs—either because the authors consider them non-essential or because they are intentionally left as exercises for the reader. However, such deliberate gaps can easily discourage learners like me, who have not received systematic training in mathematics at the college level or beyond. Fortunately, the remarkable mathematical reasoning capabilities of large language models (LLMs) come to the rescue. This blog was developed from a self-contained, step-by-step tutorial generated by ChatGPT. Throughout the learning process, I played the role of a verifier, which greatly flattened the learning curve.

As an aside, I noticed that ChatGPT first employs a kind of verbalised reinforcement learning as a high-level planner, decomposing the overall objective into manageable steps with concrete, verifiable targets (e.g., boxed key equations). This process is further refined by reinforcement learning with verifiable rewards (RLVR) techniques, which help ensure that the generated content stays on course. Even so, I was completely astonished by ChatGPT’s ability to produce LaTeX equations with such precision—almost entirely error-free. It had never occurred to me that intricate and often lengthy mathematical expressions in LaTeX format could be compressed within an LLM and then elicited so accurately. Whether or not this achievement can be considered a “jewel in the crown” of intelligence, it undeniably showcases the transformative potential of LLMs in reshaping education—for instance, through specialized textbooks collaboratively compiled by communities of learners. Moreover, LLMs enhanced with RLVR techniques have unexpectedly evolved into sophisticated sifters for navigating the overwhelming volume of knowledge and the low signal-to-noise ratio in the internet era.

Acknowledgement

This blog was developed from a self-contained, step-by-step tutorial generated by OpenAI ChatGPT, which also assisted in refining the phrasing and expressions, as well as in suggesting suitable titles.

@misc{Cai2025odelearningnotes-1,
    author = {Xin Cai},
    title = {Reconstructing the Scaffolding A Learner’s Notes on Ordinary Differential Equations: Part 1 Exploring the Picard–Lindelöf and Cauchy–Peano Theorems},
    howpublished = {\url{https://totalvariation.github.io/blog/2025/concise-intro-odes-part1/}},
    note = {Accessed: 2025-10-29},
    year = {2025}
}